응용통계학 3장 확률은 다음의 목차로 이루어져 있다.
3.1 표본공간과 사상
3.2 사상의 확률
3.3 확률법칙
3.4 조건확률
3.5 베이즈 정리
3.1 표본공간과 사상
확률의 두 가지 전제조건
i ) 어떠한 '실험이나 조사'가 있어야 함
ii ) 실험이나 조사의 '결과'가 있어야 함
1) 표본공간과 표본점
- 표본공간(Sample Space): 어떤 실험이나 조사에서 얻을 수 있는 '모든 결과의 집합', S로 표기
- 표본점(Sample Point): 표본공간에 속하는 각각의 원소
- 표본공간은 표본점의 유한성에 따라
- 유한표본공간(finite sample space): 표본점의 개수가 유한인 공간
- 무한표본공간(infinite sample space): 표본점의 개수가 무한인 공간
- 표본공간은 표본점의 종류에 따라
- 이산형 표본공간(discrete sample space): 표본점을 하나씩 셀 수 있는 표본공간
- 연속형 표본공간(continuous sample space): 표본점을 하나씩 셀 수 없는 표본공간
2) 사상
- 사상(Event): 실험이나 조사를 통해 얻을 수 있는 모든 결과 중 특정 조건을 만족하는 결과의 집합을 의미
- 표본공간 S에서 정의된 사상: 표본공간 S의 부분집합
- 사상은 표본점의 개수에 따라
- 단순사상(simple event): 표본점 하나로 이루어진 사상
- 복합사상(compound event): 둘 이상의 표본점으로 이루어진 사상
- 사상은 표본점의 유한성에 따라
- 유한사상(finite event): 유한개의 표본점으로 이루어진 사상
- 무한사상(infinite event): 무한개의 표본점으로 이루어진 사상
사상의 종류
- 결합사상(Joint Event)
사상 A와 B에 동시에 포함되는 표본점의 집합을 A와 B의 결합사상 혹은 곱사상이라 함
P(A∩B)

- 합사상(Union of Events)
사상 A에 포함되거나 혹은 사상 B에 포함되는 표본점의 집합을 A와 B의 합사상이라 함
P(AUB)

- 배반사상(Exclusive Event)
1) 2개의 사상 A, B에 대하여 A와 B의 결합사상이 공사상인 경우, A와 B는 상호 배반인 사상 혹은 간단히 배반사상
2) 3개의 사상 A, B, C에 대하여, A와 B, B와 C, C와 A가 각각 배반사상이면, 사상 A, B, C는 배반사상
3) n개의 사상 A1, A2, ..., An에 대하여 임의의 두 사상 Ai와 Aj가 배반사상이면, 사상 A1, A2, ..., An는 배반사상

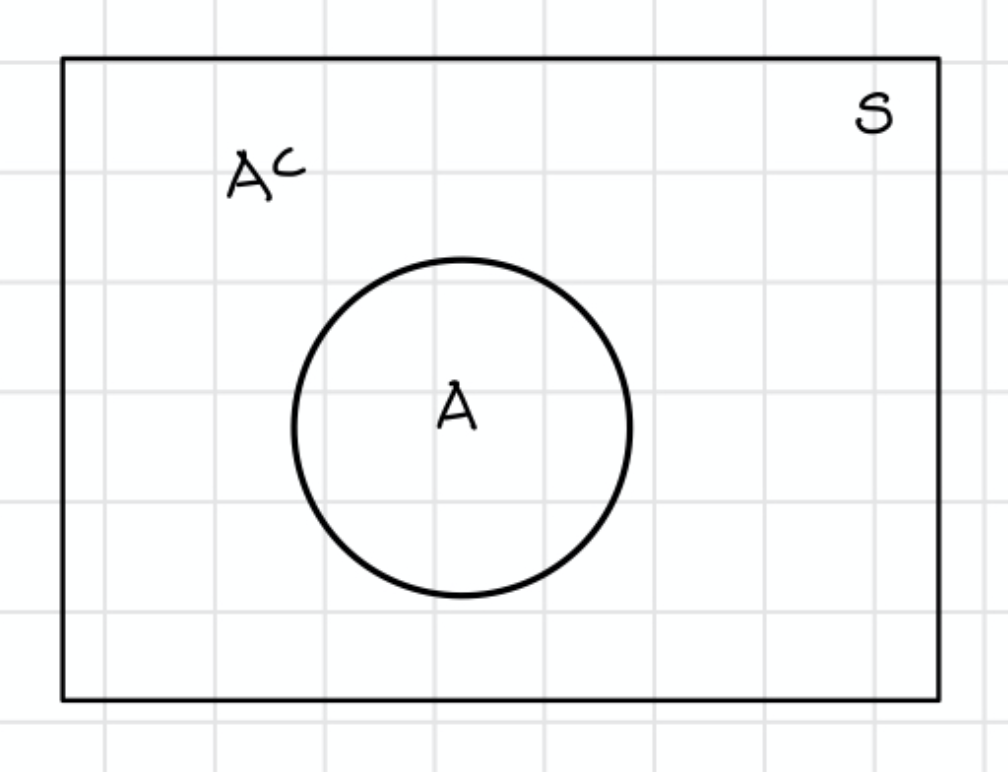
- 여사상(Complementary Event)
표본공간 S의 표본점 중 사상 A에 포함되지 않는 표본점의 집합을 A의 여사상이라 함
P(Ac)
** 사상 A와 여사상 Ac는 배반사상
3.2 사상의 확률
- 확률: 표본공간 S에서 정의된 사상 A에 대하여 A가 출현할 가능성을 수치로 나타낸 것
1. 고전적 확률(Classical Probability)
유한 표본 공간 S는 출현 가능성이 같은 N개의 표본점을 가지며,
S에서 정의된 사상 A가 n개의 표본점을 가지는 경우, 사상 A가 출현할 고전적 확률은 P(A) = n/N
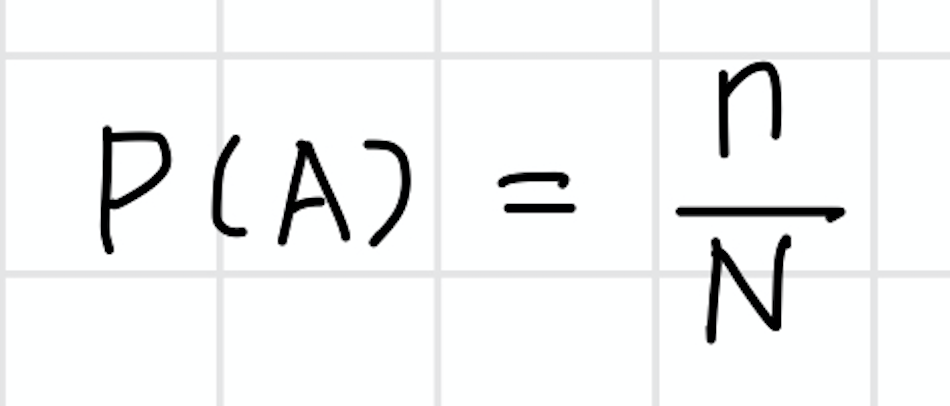
- 고전적 확률은 유한표본공간이며, 표본점의 출현 가능성이 같다는 것을 전제로 함.
- 표본점의 출현 가능성이 서로 다른 경우도 많음. 어떤 공장의 제품이 불량일 확률과 양품일 확률은 같지 않고, 공장의 불량률에 따라 좌우
2. 경험적 확률(Frequency Probability)
사상 A를 관측하는 실험을 동일한 조건에서 n번 반복하였을 때, 사상 A가 출현한 횟수는 nA라 가정.
이러한 실험을 무한히 반복하였을 때, 상대 도수 nA/n이 어떠한 수 a로 수렴하면 이 수 a를 사상 A의 경험적 확률이라 함
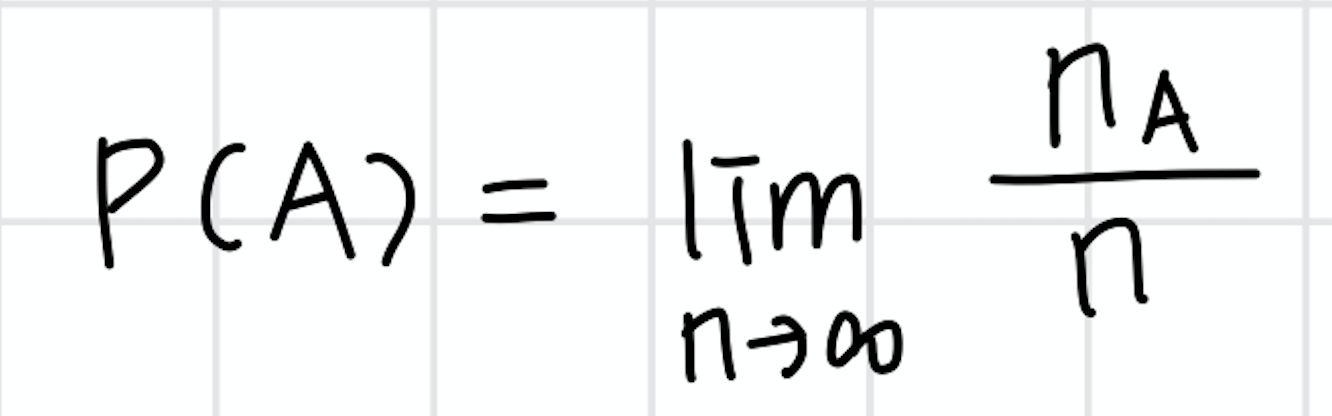
3. 공리적 확률(Axiomatic Probability)
표본공간 S에서 정의된 확률 P가 다음의 세 가지 성질을 만족할 때, 확률 P를 공리적 확률이라 함
- 모든 사상 A에 대하여 0 <= P(A) <= 1
- P(S) = 1
- 임의의 배반사상 A1, A2, ... 에 대하여

- 확률은 어떠한 경우에서도 다음 세 가지 조건을 만족해야 함.
3.3 확률법칙
1. 공사상의 확률 P(∮) = 0

2. 덧셈정리 P(AUB) = P(A) + P(B) + P(A∩B)
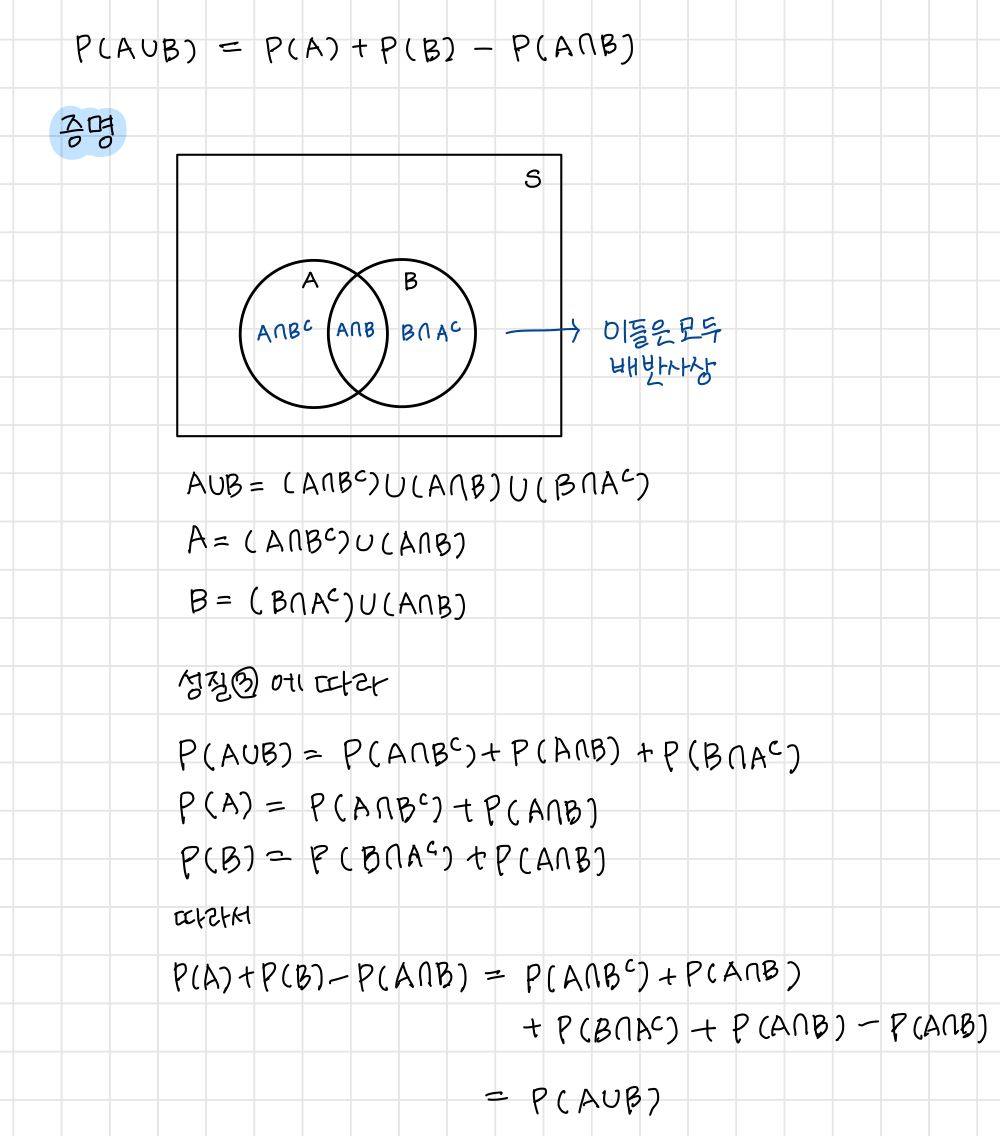
3. 여사상의 확률 P(Ac) = 1- P(A)

3.4 조건확률
예) 1개의 동전을 2회 던질 경우, P1, P2 두 확률
P1: 처음에 앞면이 나오고 나중에 뒷면이 나오는 확률 --> 사상의 동시 출현 확률, 결합확률(joint probability)
P2: 처음에 앞면이 나왔을 때 나중에 뒷면이 나오는 확률 --> '조건'의 개입, 조건확률(conditional probability)
표본 공간 S = { HH, HT, TH, TT }
처음에 앞면이 나오는 사상 A = { HH, HT }
나중에 앞면이 나오는 사상 B = { HH, TH }
P1 = P(A∩B) = 1/4
P2 = P(B | A) = P(A∩B) / P(A) = 1/2
1) 조건확률(conditional probability)
2개의 사상 A, B에 대하여 조건확률 P(B|A), P(A|B)는 아래와 같음
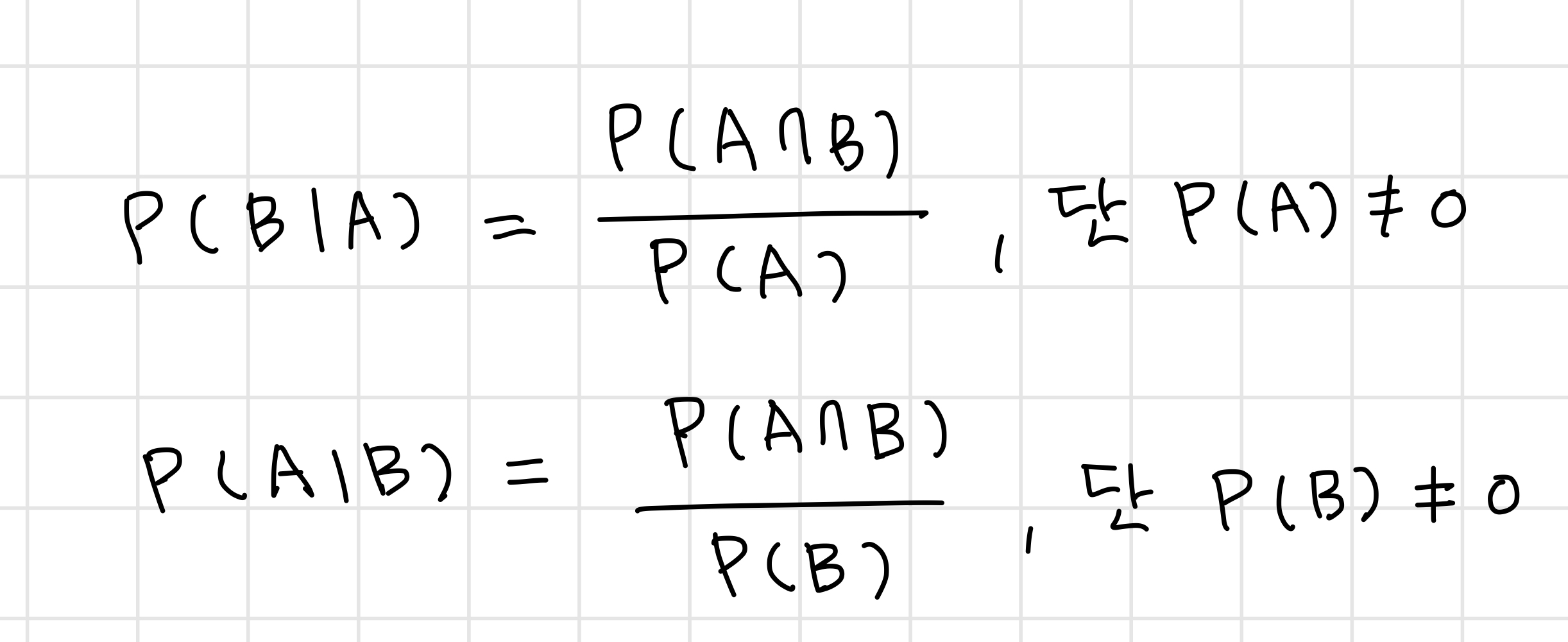
- 조건확률의 정의는 결합확률과 구분하기 위해 표현상의 모호함을 확실히 배제해야 함.
이를 테면, P2를 정의할 때에도 다음과 같이 정의할 수 있음
P2: 처음에 앞면이 나오는 조건하에서 나중에 뒷면이 나오는 확률
- 조건확률 P(B | A) 에서 A와 B는 시간상의 순서와는 상관 없음.
2) 독립사상(Independent Events)
어느 한 사상의 출현을 전제해도 나머지 사상의 출현 가능성이 변하지 않는 성질을 만족하는 사상
독립사상의 정의
(1) 2개의 사상 A, B에 대하여
P(A∩B) = P(A)P(B)
이면, 사상 A, B를 독립사상이라 함.
- 독립사상이 아닌 경우 의존사상(dependent events)이라 함.
** A, B가 독립사상인 경우, A와 B를 (서로) 독립이라 함.
(2) 3개의 사상 A, B, C에 대하여, 임의의 2개의 사상의 조합 즉, A와 B, B와 C, C와 A가 독립이고
P(A∩B∩C) = P(A)P(B)P(C)
이면, 사상 A, B, C 를 독립사상이라 함.
(3) n개의 사상 A1, A2, ..., An에 대하여 임의의 2, 3, 4, ..., n-1 개의 사상의 조합이 독립이고,
P(A1 ∩ A2 ∩ ... ∩ An) = P(A1)P(A2)...P(An)
이면, 사상 A1, A2, ..., An을 독립사상이라 함
독립사상의 증명


3.5 베이즈 정리
1. 사상의 분할(Partition of an Event)
사상 A와 공집합이 아닌 k개의 사상 B1, B2, ..., Bk 에 대하여 다음의 두 성질
1) 임의의 i ≠ j 에 대하여 Bi ∩ Bj = ∮(배반사상)
2) B1 ∪ B2 ∪ ... ∪ Bk = A
가 성립하면 사상 B1, B2, ..., Bk를 사상 A의 분할(partition) 이라 함
- 분할의 성질: 표본공간의 분할을 사용하여 다른 사상의 분할을 쉽게 구성할 수 있음
2. 전확률 정리(Theorem of Total Probability)
사상 B1, B2, ..., Bk가 표본공간 S의 분할이거나 또는 사상 A의 분할이면 A의 확률은 다음과 같다
P(A) = ∑ P(A | Bk) P(Bk)
증명) k개의 사상 B1, B2, ..., Bk가 표본공간 S의 분할이며
또한, k개의 사상 B1 ∩ A, B2 ∩ A, ..., Bk ∩ A 는 사상 A의 분할일 때,
사상 A는 다음과 같이 표현 가능.
A = (B1 ∩ A) ∪ (B2 ∩ A) ∪ ... ∪ (Bk ∩ A)
따라서 사상 A의 확률은 다음과 같이 구할 수 있음
P(A) = P{(B1 ∩ A) ∪ (B2 ∩ A) ∪ ... ∪ (Bk ∩ A)} # 배반사상의 결합확률
= P(B1 ∩ A) + P(B2 ∩ A) + ... + P(Bk ∩ A) # 조건확률
= P(A | B1)P(B1) + P(A | B2)P(B2) + ... + P(A | Bk)P(Bk)
= P(B1 | A)P(A) + P(B2 | A)P(A) + ... + P(Bk | A)P(A) # 이렇게 정리하면
= P(A){P(B1 | A) + P(B2 | A) + ... + P(Bk | A)} # 확률 값을 구하는 데에 도움이 안됨.
예제)
한 명의 대통령을 선출하는 선거에서 갑, 을, 병 3명이 출마하였다. 갑, 을, 병이 당선될 확률이 각각 0.3, 0.5, 0.2이고
당선 후 세금을 올릴 확률이 각각 0.8, 0.1, 0.4라고 할 때, 선거가 끝난 후 세금이 오를 확률은 얼마인가?
Q1 세금이 오를 확률 P(A)
당선될 확률
P(B1) = 0.3, P(B2) = 0.5, P(B3) = 0.2
당선 후 세금을 올릴 확률
P(A | B1) = 0.8, P(A | B2) = 0.1, P(A | B3) = 0.4
P(A) = ∑ P(A | Bk) P(Bk)
= P(A | B1) P(B1) + P(A | B2) P(B2) + P(A | B3) P(B3)
= 0.8 x 0.3 + 0.5 x 0.1 + 0.2 x 0.4 = 0.24 + 0.05 + 0.08
= 0.37
Q2 세금이 이미 올랐다는 조건하에 갑이 당선되었을 조건확률 P(B1 | A)
P(A | B1) = P(A ∩ B1) / P(B1)
P(A ∩ B1) = P(A | B1) P(B1)
P(B1 | A) = P(B1 ∩ A) / P(A)
= P(A | B1) P(B1) / P(A)
= 0.8 x 0.3 / 0.37 = 24/37
3. 베이즈 정리(Bayes' Rule)
B1, B2, ..., Bk가 표본공간 S의 분할이고
다른 사상 A에 대하여 P(A) ≠ 0이면, 전확률 정리에 의해 P(B1 | A)는 다음과 같다
P(Bi | A) = P(Bi ∩ A) / P(A)
= P(A | Bi) P(Bi) / ∑ P(A | Bj) P(Bj)
3장 끝!!!!!
'수학 > 응용통계학' 카테고리의 다른 글
| [응용통계학] 4장. 확률변수와 확률분포 (0) | 2021.03.28 |
|---|---|
| [응용통계학] 2장. 자료의 요약 및 정리(3) - 도표를 이용한 자료의 정리_박스 플롯(상자그림) (0) | 2021.03.08 |
| [응용통계학] 2장. 자료의 요약 및 정리(2) - 도표를 이용한 자료의 정리 (0) | 2021.02.28 |
| [응용통계학] 2장. 자료의 요약 및 정리(1) - 자료의 요약 (0) | 2021.02.23 |
| [응용통계학] 1장. 통계학 개요 (0) | 2021.02.21 |


